KDE(커널 밀도 함수 추정)
Kernel density estimation(KDE) is a way to estimate the probability density function (PDF) of a random variable in a non-parametric way.
밀도 추정 (Density Estimation)
관측된 데이터들의 분포로부터 변수의 분포 특성을 추정
어떤 변수 x의 밀도를 추정하는 것은 x의 확률밀도함수 (pdf, probability density function)을 추정하는것과 동일
Parametric vs. Non-parametric density estimation
Parametric : 미리 pdf에 대한 모델을 정해놓고 데이터들로부터 모델의 파라미터만 추정.
non-parametric : 어떠한 사전 정보나 지식 없이 순수하게 관측된 데이터만으로 확률밀도함수를 추정
Non-parametric 밀도추정의 가장 간단한 형태는 히스토그램(histogram)
관측된 데이터들로부터 히스토그램을 구한 후 구해진 히스토그램을 정규화하여 확률밀도함수로 사용.
단점 : bin의 경계에서 불연속, bin의 크기 및 시작위치에 따라 히스토그램이 달라짐, 고차원데이터에서의 메모리문제.
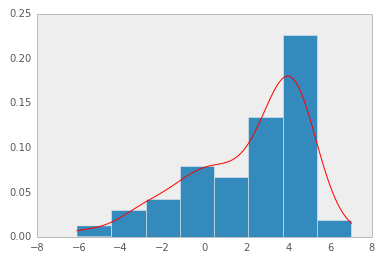
Kernel
수학적 의미로 적분값이 1인 non-negative 함수, 모든값이 대칭인 함수.
Uniform, Gaussian 등 다양한 종류의 커널이 있다.

커널 밀도 추정

1. 관측된 데이터 각각마다 해당 데이터 값을 중심으로 하는 커널 함수를 생성한다: K(x-xi)
2. 이렇게 만들어진 커널 함수들을 모두 더한 후 전체 데이터 개수로 나눈다.
scipy stat의 gaussian_kde calass를 활용하면 Gaussian kde를 구할수있다.

docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gaussian_kde.html
scipy.stats.gaussian_kde — SciPy v1.6.0 Reference Guide
D.W. Scott, “Multivariate Density Estimation: Theory, Practice, and Visualization”, John Wiley & Sons, New York, Chicester, 1992.
docs.scipy.org